Công Thức Tính Diện Tích Tam Giác Đầy Đủ: Từ Cơ Bản Đến Nâng Cao (Heron, Oxyz, Nội Tiếp & Ngoại Tiếp)

Gia Sư TutorX Học Viện
2 ngày trước
3 phút đọc

Trong chương trình Toán học phổ thông, tam giác là một trong những hình học cơ bản và xuất hiện nhiều trong các dạng bài tập từ cấp 2 đến luyện thi THPT. Để giải nhanh và chính xác các bài toán, học sinh cần nắm chắc công thức tính diện tích tam giác.

Ở bài viết này, TheTutorX sẽ tổng hợp chi tiết tất cả công thức, từ cơ bản đến nâng cao, kèm ví dụ minh họa để bạn dễ dàng áp dụng.

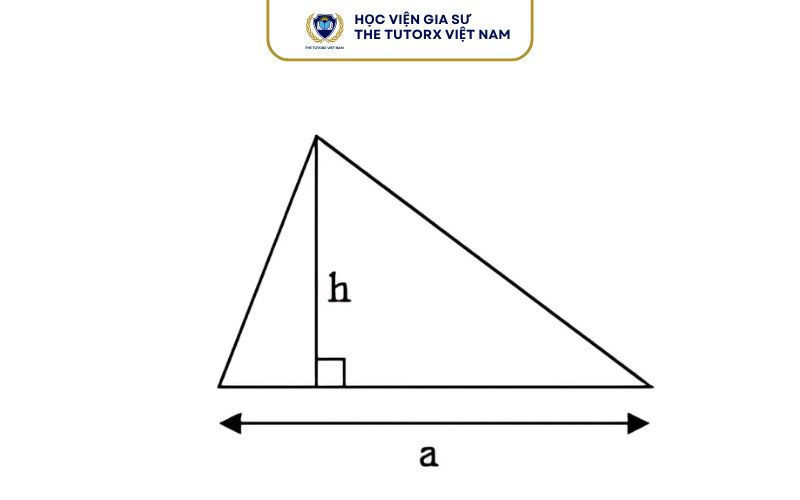
1. Công thức diện tích tam giác cơ bản

Công thức chung để tính diện tích tam giác khi biết đáy và chiều cao:

S=a×h2S = \frac{a \times h}{2}S=2a×h

Trong đó:

aaa: độ dài cạnh đáy
hhh: chiều cao tương ứng

Ví dụ: tam giác có đáy 8cm, chiều cao 6cm → S=8×6/2=24cm2S = 8 \times 6 / 2 = 24cm^2S=8×6/2=24cm2.

2. Công thức diện tích tam giác vuông

Với tam giác vuông, hai cạnh góc vuông đóng vai trò là đáy và chiều cao.

S=a×b2S = \frac{a \times b}{2}S=2a×b

Ví dụ: tam giác vuông có cạnh góc vuông a=3cm, b=4cm → S=6cm2S = 6cm^2S=6cm2.

3. Công thức diện tích tam giác vuông cân

Đây là trường hợp đặc biệt khi hai cạnh góc vuông bằng nhau:

S=12×a2S = \frac{1}{2} \times a^2S=21×a2

Nếu a = 5cm → S=12.5cm2S = 12.5cm^2S=12.5cm2.

4. Công thức diện tích tam giác cân và tam giác đều

Với tam giác cân: vẫn áp dụng công thức (a×h)/2(a \times h)/2(a×h)/2.
Với tam giác đều:
S=a234S = \frac{a^2 \sqrt{3}}{4}S=4a23

Ví dụ: tam giác đều cạnh 6cm → S=93cm2S = 9\sqrt{3}cm^2S=93cm2.

5. Công thức Heron (biết 3 cạnh)

Nếu tam giác có 3 cạnh a,b,ca, b, ca,b,c:

p=a+b+c2p = \frac{a + b + c}{2}p=2a+b+cS=p(p−a)(p−b)(p−c)S = \sqrt{p(p-a)(p-b)(p-c)}S=p(p−a)(p−b)(p−c)

Ví dụ: tam giác có cạnh a=3, b=4, c=5 → p=6p=6p=6, S=6×3×2×1=6cm2S = \sqrt{6 \times 3 \times 2 \times 1} = 6cm^2S=6×3×2×1=6cm2.

6. Công thức trong không gian Oxyz

Khi tam giác được xác định bởi 3 điểm A, B, C trong hệ trục Oxyz:

S=12×∣AB⃗×AC⃗∣S = \frac{1}{2} \times |\vec{AB} \times \vec{AC}|S=21×∣AB×AC∣

Đây là công thức nâng cao, thường dùng trong hình học không gian lớp 12.

7. Công thức liên quan đến đường tròn nội tiếp và ngoại tiếp

Dùng bán kính đường tròn nội tiếp rrr:
S=p×r2S = \frac{p \times r}{2}S=2p×r
Dùng bán kính đường tròn ngoại tiếp RRR:
S=abc4RS = \frac{abc}{4R}S=4Rabc

8. Các lưu ý khi áp dụng công thức diện tích tam giác

Xác định chính xác loại tam giác.
Đổi đơn vị trước khi tính (m, cm, mm).
Kiểm tra điều kiện tồn tại tam giác (a + b > c).
Với bài nâng cao, nắm chắc vector và tọa độ.

9. Ví dụ tổng hợp

Tam giác có cạnh a=7cm, b=8cm, c=9cm.

p=(7+8+9)/2=12p = (7+8+9)/2 = 12p=(7+8+9)/2=12.
S=12×(12−7)(12−8)(12−9)=12×5×4×3=720≈26.83cm2S = \sqrt{12 \times (12-7)(12-8)(12-9)} = \sqrt{12 \times 5 \times 4 \times 3} = \sqrt{720} ≈ 26.83cm^2S=12×(12−7)(12−8)(12−9)=12×5×4×3=720≈26.83cm2.

10. Kết luận

Nắm vững công thức diện tích tam giác là nền tảng giúp học sinh tự tin giải nhiều dạng bài khác nhau. Để học tập hiệu quả hơn, hãy tham khảo thêm các bài giảng chi tiết và tài liệu tại:

👉 Công thức diện tích tam giác – TheTutorX